Asymptotická složitost

Opakování matematiky

• číselné obory: $\mathbb{N}, \mathbb{Z}, \mathbb{R}$
• funkce: $f: A \to B$
• výroková logika: $\neg, \land, \lor, \to, \leftrightarrow$
• predikátová logika: $\forall, \exists$
• množiny: $A \cup B, A \cap B, A \setminus B$

Asymptotická složitost

Asymptotická složitost

Asymptotická složitost je matematický model, který umožňuje popsat chování algoritmu v závislosti na velikosti vstupních dat.

Důvod existence

• porovnání algoritmů
• odhad výpočetního času
• odhad výpočetní paměti

Složitosti

• časová složitost — maximální počet provedených operací
• paměťová složitost — maximální počet použitých paměťových buněk

Notace

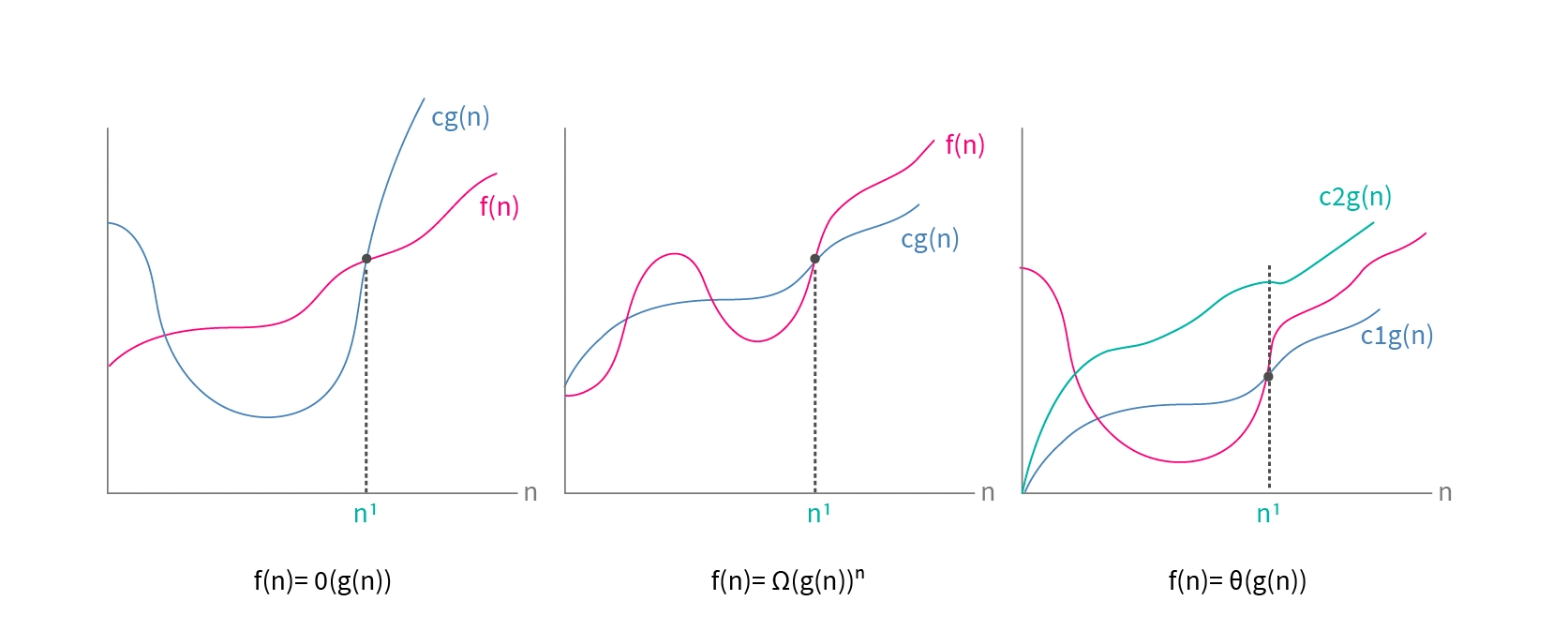
• $O$ — $\exists c \in \mathbb{R}^+, \exists n_0 \in \mathbb{N}, \forall n \geq n_0: f(n) \leq c \cdot g(n)$
• $o$ — $\forall c \in \mathbb{R}^+, \exists n_0 \in \mathbb{N}, \forall n \geq n_0: f(n) < c \cdot g(n)$
• $\Omega$ — $\exists c \in \mathbb{R}^+, \exists n_0 \in \mathbb{N}, \forall n \geq n_0: f(n) \geq c \cdot g(n)$
• $\omega$ — $\forall c \in \mathbb{R}^+, \exists n_0 \in \mathbb{N}, \forall n \geq n_0: f(n) > c \cdot g(n)$
• $\Theta$ — $\exists c_1, c_2 \in \mathbb{R}^+, \exists n_0 \in \mathbb{N}, \forall n \geq n_0: c_1 \cdot g(n) \leq f(n) \leq c_2 \cdot g(n)$

Klasické složitosti

• $O(1)$ — konstantní složitost
• $O(\log n)$ — logaritmická složitost
• $O(n)$ — lineární složitost
• $O(n \log n)$ — lineárně logaritmická složitost
• $O(n^2)$ — kvadratická složitost
• $O(n^3)$ — kubická složitost

Chování velkého O

• $2 \in O(1)$
• $2 \cdot n^2 + 3 \in O(n^2)$
• $\frac{x^2 + 3x + 2}{x + 1} \in O(x)$
• $2^{n + 1} \in O(2^n)$
• $3 + 2 \cdot n \cdot \log n \in O(n \cdot \log n)$

Chování dalších notací

• $2 \in o(n)$
• $2 \in o(n!)$
• $n \in \Omega(1)$
• $n \in \Omega(\log n)$
• $n \in \omega(1)$
• $n^2 \in \Theta(n^2)$
• $5n^3 + 2n^2 + 300 \in \Theta(n^3)$

Procvičování

Hvězdy 1

Kolik hvězd bude vypsaných po spuštění programu? Kolik kroků program provede? Kolik to bude v notaci $O$?

star1(n):
    for i:=1 to n do
        for j:=1 to n do
            print "*"

Hvězdy 2

Kolik hvězd bude vypsaných po spuštění programu? Kolik kroků program provede? Kolik to bude v notaci $O$?

star2(n):
    for i:=1 to n do
        for j:=1 to i do
            print "*"

Hvězdy 3

Kolik hvězd bude vypsaných po spuštění programu? Kolik kroků program provede? Kolik to bude v notaci $O$?

star3(n):
    while n > 0 do
        print "*"
        n := n/2

Hvězdy 4

Kolik hvězd bude vypsaných po spuštění programu? Kolik kroků program provede? Kolik to bude v notaci $O$?

star4(n):
    while n > 0 do
        if (n is odd) then
            print "*"
        n := n/2

Rekurze

Kolik kroků program provede? Kolik to bude v notaci $O$?

rekurze(n):
    if n = 0 then
        return 0
    else
        return rekurze(n-1) + 1

Reverzní přístup

Vymyslete algoritmy v pseudokódu, které budou mít následující asymptotické složitosti:

• $O(1)$
• $O(n^3)$
• $O(n \log n)$
• $O(n!)$